怎样增强数学水平?想要数学拔尖有哪些方法?
平时有很多同学在数学学习过程中已经有了的基础和水平,但是想要在数学学习中成为尖子生,就需要平时的学习中增强自己的能力和思维。秦学四川网的小编帮助大家整理了一些在平时学习中增强数学能力的学习方法。同学们可以在完成自己固定的学习任务之后,用的业余时间下意识的运用这些方法去锻炼自己的学习能力。下面就是学习方法的具体内容,一起来看看吧:

一、提升运算的熟练了、综合度和难度。
运算始终是数学学习的基础,运算能力的强弱直接决定了做题的速度和成绩的高低。对于基础不错的学生来说,基础运算肯定是没有问题了,那么就需要在运算的熟练度、综合度和难度方面下功夫。
1、做一些技巧性简算。
2、化简求值中的整体代入求值。
3、乘法公式的变形应用。
4、形式比较复杂的方程。
5、含字母参数的不等式(组)的解法。
6、比较复杂的分式的化简。
7、的化简计算。
8、等式的等价变形和证明。
9、定义新运算。
10、比较复杂的因式分解。
11、根与系数的关系。
12、十字相乘法。
……
运算题目不仅仅锻炼的是运算能力,对学生的注意力、观察力、思维能力等都是有帮助的,能培养和提生的综合学习力。
二、注意去总结做题的思路,方法和技巧。
在平时的学习中要多去总结和思考,特别是在数学的解题中会有一些技巧性的东西,如果能在平时能总结出并且去运用,就会提升在考试时做题的速度和效率,能更快的找到思路。
很多基础中等的同学所面临的较大问题就是在解题中不会分析,找不到冲刺口。在平时的学习中都会有这样的经历和体验,一道题目自己苦思冥想了很久也不能解答,当老师稍微提示后就理解了,会感到很惊讶原来这么简单,我为什么没有想到呢?
因此在解题中关键的关键就在于找到解题的冲刺口,解题的冲刺口就需要我们我们去总结、归纳和运用,并形成的条件反射,看到一个条件就能想到相关的知识点、方法、思路和技巧。
举一个简单的例子,看到角平分线我们都能想到相等的角以及角的和差倍分关系,看到平行线就能想到相等的角或互补的角,那么将两者相结合呢?
出现一条角平分线外加平行,一般会出现等腰三角形,
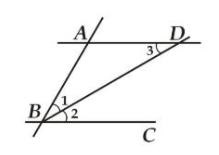
出现两条角平分线外加一组平行线就会出现直角三角形。
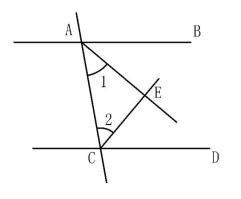
这也就是常见的一些几何模型,掌握几何模型对我们在解题过程中寻找思路和方法有帮助。
三、掌握常见额数学思想的内涵、适用条件及使用方法和技巧。
数学思想方法是把知识转化为能力的桥梁,是解题规律的总结,是达到以点带面、触类旁通、摆脱题海的有效之路.因此我们应抓住临近中考的这段时间,去研究、归纳、熟悉那些常用的解题方法与技巧,从而为夺取中考搭起灵感和智慧的平台.
简单阐述一下初中数学学习中常用的几种数学思想和方法:
1、方程思想:

2、函数思想:

3、数形结合思想

4、分类讨论思想
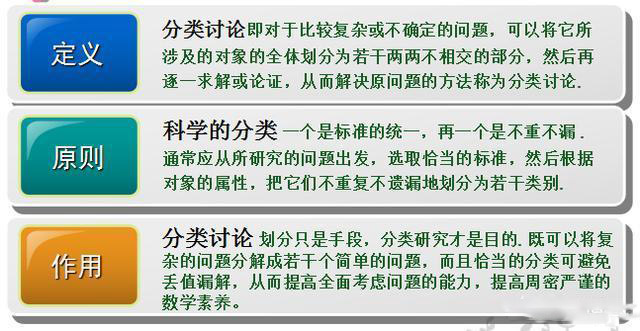
- 热门课程
- 热门资讯
- 热门资料
- 热门福利
-
 高中补哪个科目比较好?渭南伊顿教育高中小班课辅导高中补哪一门科目比较好?这是很多家长都非常关心的一个问题,众所周知,高中的各个学科学习内容难度都是比较大的,时间各方面也都比较紧张,所以要不要补课,怎么补课都是需要根据实际情况来决定的。 一、高中补哪个科目比较好? 小编觉得高中每个阶段的侧重点都是不一样,但是对于语文、数学、英语这三门主科要
高中补哪个科目比较好?渭南伊顿教育高中小班课辅导高中补哪一门科目比较好?这是很多家长都非常关心的一个问题,众所周知,高中的各个学科学习内容难度都是比较大的,时间各方面也都比较紧张,所以要不要补课,怎么补课都是需要根据实际情况来决定的。 一、高中补哪个科目比较好? 小编觉得高中每个阶段的侧重点都是不一样,但是对于语文、数学、英语这三门主科要 -
 “披荆斩棘”的意思是什么呢?成语故事的来源是什么?“披荆斩棘”比喻在创业过程中或前进道路上清除障碍,克服重重困难。那么,对于它的出处来源,大家了解多少呢?下面就一起来跟小编来一起仔细了解一下这个四字成语吧! 一、“披荆斩棘”的意思是什么呢? 拼音:pī jīng zhǎn jí 解释:劈开丛生多刺的野生植物。比喻在创业过程中或前进道路上清
“披荆斩棘”的意思是什么呢?成语故事的来源是什么?“披荆斩棘”比喻在创业过程中或前进道路上清除障碍,克服重重困难。那么,对于它的出处来源,大家了解多少呢?下面就一起来跟小编来一起仔细了解一下这个四字成语吧! 一、“披荆斩棘”的意思是什么呢? 拼音:pī jīng zhǎn jí 解释:劈开丛生多刺的野生植物。比喻在创业过程中或前进道路上清 -
 陕西艺考文化课补习学校推荐相信很多艺考生都有这样的困扰,自己的专业课一点都不担心,但是文化课学习却提升困难,特别是现在艺考政策的变化,文化课成绩的比重在录取当中也是逐渐提升,如何快速补齐文化课短板成为众多艺考生最关心的问题,下面小编就给大家来推荐几个陕西艺考文化课补习学校。 1、西安西工大补习学校 西工大补习学校主要
陕西艺考文化课补习学校推荐相信很多艺考生都有这样的困扰,自己的专业课一点都不担心,但是文化课学习却提升困难,特别是现在艺考政策的变化,文化课成绩的比重在录取当中也是逐渐提升,如何快速补齐文化课短板成为众多艺考生最关心的问题,下面小编就给大家来推荐几个陕西艺考文化课补习学校。 1、西安西工大补习学校 西工大补习学校主要 -
 “讽”怎么读?组词有哪些?“讽”组词造句有哪些?“讽”这个字,读“fěng”,可能大家对于它比较熟悉的组词就是“讽喻”“讽诵”“嘲讽”,那么大家知道关于这个字都能组哪些词吗?今天小编就给大家整理了一部分关于“讽”的相关组词,一起来看看吧! 一、“讽”怎么读?组词有哪些? 拼音:fěng 解释:1. 动词 用含蓄尖刻的话批评、劝告或讥笑。
“讽”怎么读?组词有哪些?“讽”组词造句有哪些?“讽”这个字,读“fěng”,可能大家对于它比较熟悉的组词就是“讽喻”“讽诵”“嘲讽”,那么大家知道关于这个字都能组哪些词吗?今天小编就给大家整理了一部分关于“讽”的相关组词,一起来看看吧! 一、“讽”怎么读?组词有哪些? 拼音:fěng 解释:1. 动词 用含蓄尖刻的话批评、劝告或讥笑。
-
 中考各科最实用答题规范!语文数学英语都有!中考各科最实用答题规范!语文数学英语都有!很多考生在考试答题的时候,经常会因为一些自己的小习惯导致被扣分,或者是没有一些良好的习惯,导致答题的时候会有一些失误。对于这些学生来说,自身的学习能力和知识水平其实并没有什么问题,只要注意好这些答题时候的小问题,就可以让成绩跟上一层楼。小编给大家总结了中
中考各科最实用答题规范!语文数学英语都有!中考各科最实用答题规范!语文数学英语都有!很多考生在考试答题的时候,经常会因为一些自己的小习惯导致被扣分,或者是没有一些良好的习惯,导致答题的时候会有一些失误。对于这些学生来说,自身的学习能力和知识水平其实并没有什么问题,只要注意好这些答题时候的小问题,就可以让成绩跟上一层楼。小编给大家总结了中 -
 15本适合准高中生暑期阅读的好书!作文积累素材!15本适合准高中生暑期阅读的好书!作文积累素材!很多高中生在高中学习的过程中会面临一个问题,就是在语文学习的过程中,会遇到写作文很少有写作素材的情况。这种情况其实就是因为日常积累的素材比较少,在写作文的时候没有内容可以写,所以才会导致语文作文写作的时候遇到困难,觉得写不出作文或者作文很难写。那么
15本适合准高中生暑期阅读的好书!作文积累素材!15本适合准高中生暑期阅读的好书!作文积累素材!很多高中生在高中学习的过程中会面临一个问题,就是在语文学习的过程中,会遇到写作文很少有写作素材的情况。这种情况其实就是因为日常积累的素材比较少,在写作文的时候没有内容可以写,所以才会导致语文作文写作的时候遇到困难,觉得写不出作文或者作文很难写。那么 -
 中考数学压轴题解题技巧以及五大解题策略!中考数学压轴题解题技巧以及五大解题策略!中考数学对于很多考生来说是非常痛苦的,感觉知识点好像都掌握了,但是并不能取得很好的考试成绩。小编分析了一下有可能是因为解题技巧以及思路方面的问题,这些问题其实也相对比较好解决。小编从网上整理了一些这方面的解题技巧和解题策略。为中考数学有需求的学生带来。感兴
中考数学压轴题解题技巧以及五大解题策略!中考数学压轴题解题技巧以及五大解题策略!中考数学对于很多考生来说是非常痛苦的,感觉知识点好像都掌握了,但是并不能取得很好的考试成绩。小编分析了一下有可能是因为解题技巧以及思路方面的问题,这些问题其实也相对比较好解决。小编从网上整理了一些这方面的解题技巧和解题策略。为中考数学有需求的学生带来。感兴 -
 中考数学8大类61个易错知识点!中考数学8大类61个易错知识点!中考目前甚至已经比高考的难度要更胜一层楼,所以中考的考试对于很多考生来说也是难上加难。数学也是考试中比较难的部分,也是会拉开很多学生分数的部分。小编也是了解到大家对于数学学习都有一定的困难,其实把握好以下的知识点,考试就会很容易。小编帮助大家整理了一下中考数学中容
中考数学8大类61个易错知识点!中考数学8大类61个易错知识点!中考目前甚至已经比高考的难度要更胜一层楼,所以中考的考试对于很多考生来说也是难上加难。数学也是考试中比较难的部分,也是会拉开很多学生分数的部分。小编也是了解到大家对于数学学习都有一定的困难,其实把握好以下的知识点,考试就会很容易。小编帮助大家整理了一下中考数学中容


















 All right reserved
All right reserved
